Highly excited Rydberg states and hydrogen recombination:

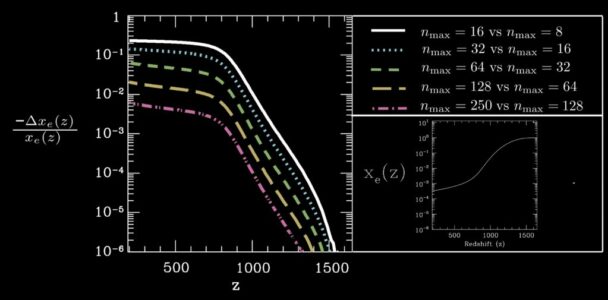
Properly interpreting precise CMB data (like that obtained from the Planck mission) requires a precise treatment of atomic hydrogen recombination (the formation of the first atoms at redshift (. Working with Chris Hirata, I computed the recombination of atomic hydrogen including very highly excited Rydberg states of hydrogen, establishing that the computation is sufficiently converged for cosmological parameter inference by the Planck CMB anisotropy mission if the maximum principal quantum number included in the calculation obeys $n >128&bg=fbecd8 $.

Results published in arXiv (http://arxiv.org/abs/0911.1359) and Physical Review D81:083005.

The well-known pattern of bumps and wiggles in the CMB angular power spectrum comes from acoustic oscillations in the baryon-photon plasma before primordial hydrogen first becomes neutral (‘recombination’). In order to properly interpret precision measurements of CMB power spectra and infer primordial initial conditions (as described by the power spectrum of density fluctuations ) and cosmological parameters (e.g.  the baryon density ), the recombination history must be computed to precision, in turn requiring the inclusion of highly excited states with n>100 in the recombination computation. The question of convergence is difficult, due to the breakdown of statistical equilibrium between different angular momentum states at late times; As a result, the relative populations of thousands of atomic hydrogen states must be followed separately. In the figure below, we remind the reader on the left that the energy levels of the hydrogen atom at fixed principal quantum number also consist of many angular momentum states. On the right, we show representative deviations from statistical equilibrium between different angular momentum states.

To address this question, I (in collaboration with Prof. Chris Hirata) exploited dipole selection rules and sparse matrix techniques to include states as high as n=300, separately follow all relevant states, and thus made precision recombination calculations computationally tractable using a new code called RecSparse. We included output from this code in a modified version of the CMB anisotropy code CMBFast, establishing (using a Fisher-matrix analysis) that hydrogen recombination is converged well enough for Planck data analysis for a maximum n value of n>128. RecSparse is also the first recombination code to include electric quadrupole transitions. Subsequent work by Jens Chluba confirmed our conclusions.